Assignment2: Machine Learning and KDD,
Decision Trees, and Neural Networks
Dr. Eick's Graduate AI-class (COSC 6368)
Deadlines: problem 6, 8, 9: Tu., Oct. 15 in class; problem 7: Th., October 31 in class.
last updated: September 30, 7:50p
Value: 100 (6:6, 7:70 8:12 9:12)
Problems 6, 8, 9 are "short" paper and pencil problems, wheras in problem 7 you will
you will get some exposure with respect to "making sense of data" and you will also
use a data mining tool.
Problem 6 --- Information Gain Heuristic
We would like to predict the gender of a person based on two binary attributes:
leg-cover (pants or skirts) and beard (beard or bare-faced). We assume we have a data set of
20000 individuals, 10000 of which are male and 10000 of which are female. 80% of the 10000 males
are barefaced. Skirts are present on 50% of the females. All females are bare-faced and
no male wears a skirt.
A. Compute the information gain of using the attribute leg-cover for predicting gender!
B. What is the information gain of using the attribute beard to predict gender?
C. Based on yours answers to A and B which attribute should be used as the root of a
decision tree that predicts the gender of a person?
Problem 7 --- Knowledge Discovery for the NBA using Decision Trees
The goal of this project is to explore how decision tree
tools can help in predicting the free throw percentage (FT) of a basketball
player using the following NBA-Player
Data Set and the popular decision tree tool C5.0. Free throw percentages
are considered to be either
HIGH (80% and more), and LOW (less than 80%). The NBA dataset has been
converted into the following C5.0 processable raw NBA data set
with the following NBA data set attribute definitions. Go to
the
C5.0 website and download and install
the system on your own computer. More
information about decision trees
can be found by following the above link.
A. Data set preparation for 4-fold cross validation:
When evaluating the (testing) accuracy of decision trees
to predict "good" free throw shooters use 4-fold cross validation. Take the raw nba
data set and partion it into 4 disjoint data sets of approximately equal size and with positive and negative
examples occuring with approximately the same percentages. Create 4 training sets using the union of
3 of the 4 sets, and use the remaining set as the test set for this training set.
B. Find the best pruning parameter settings: Run C5.0 with various pruning options and try
to find the "best" parameter setting that results in the highest accuracy for the classification
problem. In this project accuracy is defined as average testing performance for the 4 training
sets you constructed in step A. Explain how your "best" pruning parameter setting was
obtained; moreover, report accuracy, training performance, and average decision tree
size for the "best" and 4 other pruning parameter settings.
C. Sensitivity analysis for the obtained results:
Now look at the 4 decision trees that were obtained by running C5.0 with the "best" pruning parameter setting
(you determined in step B) for the 4 training sets. Additionally, create a fifth decision tree by running C5.0
for the complete nba data set (that contains all 184 examples) with the "best" parameter setting (include these
five decision trees in your report). Compare the 5 decision trees --- are they similar or do the look
significantly
different? What commonalities do they share and in what aspect are they different? What conclusion
do you draw from your answers to the previous questions?
D. Final Evaluation:
What did you learn from the experiments in steps B and C? What do the results tell
us about
the classification problem we are trying to solve;
e.g. did the decision tree approach work well/work badly for the problem at hand; did
you find anything interesting that distinguishes successful free throw shooters from not so
successful ones in
the NBA (e.g. is there anything nba scouts can learn from your results)? Did your results
match your expectations?
Discuss and summarize your results and findings in a
5-6 page (single spaced)
report. Include the 5 decision trees you obtained in Step C as an appendix in the report
(you can refer to the figures in your report).
Problem 8 --- Neural Networks
Give a neural network (having an architecture of your
own choice) that uses the step
activation function (your are not allowed to use other activation functions) and computes the
following function f based on inputs A, B, and C (X=f(A,B,C)):
| A | B | C | X
|
|---|
| 0 | 0 | 0 | 1
|
|---|
| 0 | 0 | 1 | 1
|
|---|
| 0 | 1 | 0 | 0
|
|---|
| 0 | 1 | 1 | 1
|
|---|
| 1 | 0 | 0 | 0
|
|---|
| 1 | 0 | 1 | 0
|
|---|
| 1 | 1 | 0 | 0
|
|---|
| 1 | 1 | 1 | 0 |
|---|
Show how your neural network computes the answer
for the third and fourth example.
Problem 9 --- Perceptron and Backpropagation Learning Algorithms
Assume we have theperceptron that is depicted in Fig. 1 that has two regular inputs, X1 and X2, and an
extra fixed input X3, which always has the value 1.
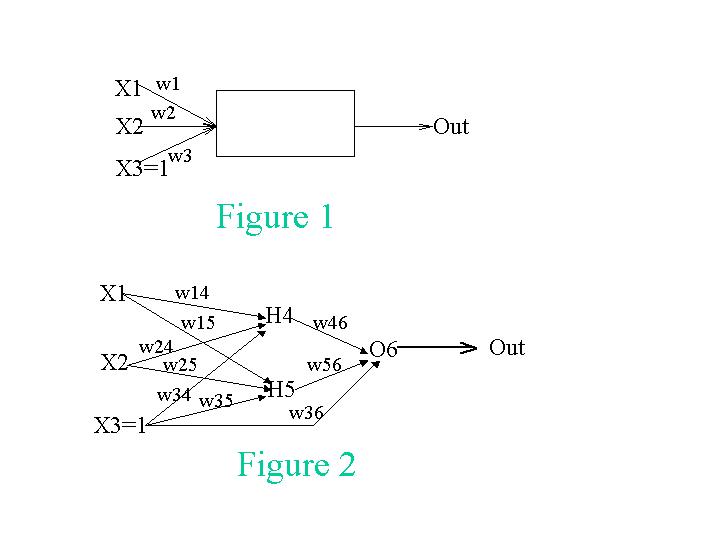The perceptron's output is given as the function:
Out= If (w1*X1 + w2*X2 + w3*X3) > 0 then 1 else 0
Note that using the extra input, X3, we can achieve the same effect as changing the
perceptron's threshold by changing w3. Thus, we can use the same simple perceptron
learning rule presented in our textbook to control this threshold as well.
A. We want to teach the perceptron to recognize the function X1 XOR X2 with the
following training set:
| X1 | X2 | X3 | Out
|
|---|
| 1 | 1 | 1 | 0
|
|---|
| 0 | 1 | 1 | 1
|
|---|
| 1 | 0 | 1 | 1
|
|---|
| 0 | 0 | 1 | 0 |
|---|
Show the change in the weights of the perceptron for every presentation of a training
instance. Assume the initial weights are: w1=0.2, w2=0.2, w3=0.2
Important: Do the iterations according to the order of the samples in the training
set. When you finish the four samples go over them again. You should stop the
iterations once you get convergence, or when the values you get indicate that there
will be no convergence. In either case explain your decision to stop the iterations.
Assume in your computations that the learning rate a is 0.2.
| Sample# | X1 | X2 | X3 | Output | True_Out | Error | w1 | w2 | w3
|
|---|
| 0 | | | | | | | 0.2 | 0.2 | 0.2
|
|---|
| 1 | 1 | 1 | 1 | | 0
|
|---|
| 2 | 0 | 1 | 1 | | 1
|
|---|
| 3 | 1 | 0 | 1 | | 1
|
|---|
| 4 | 0 | 0 | 1 | | 0
|
|---|
| 5 | 1 | 1 | 1 | | 0
|
|---|
| 6 | ... | ... | ... | ... | ... | ... | ... | ...
|
|---|
| 7 |
|
|---|
| 8 |
|
|---|
| ...
|
|---|
B. This time, instead of being limited to a single perceptron, we will introduce hidden
units and use a different activation function. Our new network is depicted in Fig. 2.
Assume that the initial weights are w14 = 0.3, w15 = 0.1, w24 = 0.2, w25 = 0.6,
w34 = 0.1, w35 = 0.1, w36 = 0.1, w46 = 0.5, and w56 = 0.2. The training set is the
same as in (a). Use g=0.1 as your learning rate.
Show what the new weights would be after using the backpropagation algorithm
for two updates using just the first two training instances. Use g(x) = 1/(1+e**(-x)) as the activation
function; that is g'(x)=(e**(-x))/(1+e**(-x))**2).
| S# | X1 | X2 | X3 | Out | True_Out | Error | w14 | w15 | w24 | w25 | w34 | w35 | w36 | w46 | w56
|
|---|
| 0 | | | | | | | 0.3 | 0.1 | 0.2 | 0.6 | 0.1 | 0.1 | 0.1 | 0.5 | 0.2
|
|---|
| 1 | 1 | 1 | 1 | | 0
|
|---|
| 2 | 0 | 1 | 1 | | 1
|
|---|
C. Will the perceptron you used for problem A ever learn the XOR function? What about
the multi-layered neural network you used when you solved problem B? Give reasons for your answers!