Experiments

 

 

 

Experiment No. 4: BCD Adders

 

Objectives
  • In this experiment, you will become familiar with the Binary-Coded-Decimal (BCD) number representation system and build a 1-digit BCD adder using 4-bit ripple-carry adders built in Lab 3.
  • You will then build a 2-digit BCD adder using two 1-digit BCD adders.

Discussion

In the BCD representation system each digit is encoded into its binary equivalent with four (4) bits.  (Why are no more or no less number of bits used?).
 

Decimal

BCD

0

0000

1

0001

2

0010

3

0011

4

0100

5

0101

6

0110

7

0111

8

1000

9

1001

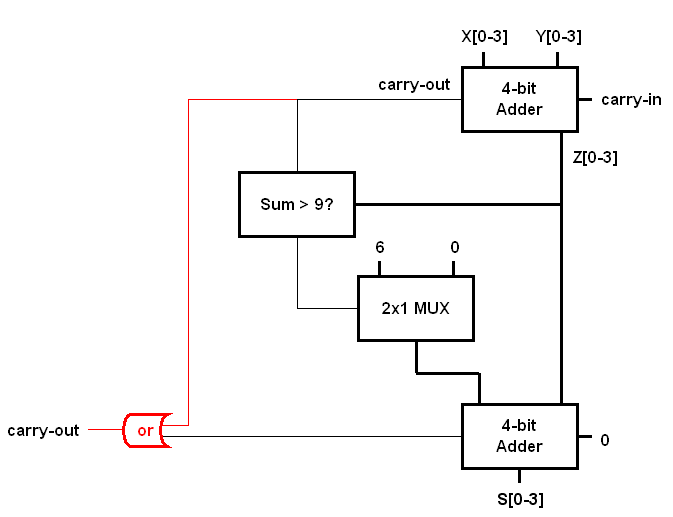
Observe that only 10 of the 16 possible bit-patterns are used in BCD.  That means the remaining 6 patterns could be treated as don't-care cases. 

For the arithmetic addition of two decimal digits in BCD, the maximum value that may be produced as the result  is 9 + 9 + 1 = 19 (two largest operands plus the carry). If we try to add two decimal digits in BCD with a 4-bit ripple-carry adder we will get a binary sum ranging from 0 to 19. When the binary sum is less than or equal to 9, it also correctly represents the sum in BCD.  When the binary sum is greater than 9, however, it does not represent the correct BCD sum. The sum in BCD is to be obtained by adding 6 to it. 

Perform the following addition in BCD as explained above:

1) 7 + 4 
2) 3 + 2 
3) 9 + 9 

The above examples should help you realize when the conversion is necessary and what should be done to perform the conversion correctly. 

Here is a block diagram of a 1-digit BCD adder
 

 

Complete the truth table below. 
 

Inputs

 

Binary Sum

 

BCD Sum

 

Decimal Number

Cin

X

Y

 

Cout

Z

 

Cout

S

 

 

0

0000

0000

 

0

0000

 

0

0000

 

0

0

0000

0001

 

0

0001

 

0

0001

 

1

0

0001

0001

 

 

 

 

 

 

 

 

0

0101

0100

 

 

 

 

 

 

 

 

0

0101

0101

 

 

 

 

 

 

 

 

0

0101

0110

 

 

 

 

 

 

 

 

0

1000

1000

 

1

0000

 

1

0110

 

16

0

1000

1001

 

 

 

 

 

 

 

 

0

1001

1001

 

 

 

 

 

 

 

 

1

1001

1001

 

 

 

 

 

 

 

 


 

 Prelab
  • Complete the truth table in the Theory section.
  • Upon an inspection of the 1-digit BCD adder block diagram shown above, you should notice that the only block you do not have a circuit for is the “Sum > 9”? block. (MAX+plus II has a prebuilt circuit for a 2x1 Multiplexor called 21mux in the mf symbol library if you need it. Yes, you can build the same BCD adder without using multiplexors, but you will need to explain your circuit in the Circuits Built section of you lab report.) Design the circuit to perform this function. (Hint: Create the truth table and use K-maps to simplify the circuit.) You will need to show your work. Having the circuit just magically appear on your circuit diagrams and saying you got it from the book will not be good enough.

 Procedure
  1. Using the table and block diagram above, build a 1-digit BCD adder using two 4-bit ripple-carry adders and possibly some other logic gates. Create a folder on your disk and name it Lab5. Copy the 4-bit adder you created in Lab 3 to the Lab4 folder. You will need to copy the following files:


 

    • 4bitadder.sym 
    • 4bitadder.gdf 
    • fa.gdf 
    • ha.gdf 


Make sure that your 1-digit BCD adder gives the correct values. (Verify with your table and resolve any differences by correcting your circuit. Note: you don't have to simulate all the different possibilities, just the ones in the table above.) Save this project as 1digitBCD in the folder Lab4. Create a default symbol for the 1-digit BCD adder for use in the next step.

Note: You can use the gnd symbol to simulate a zero, and the vcc symbol to simulate a one, if necessary.
 

  1. Build a 2-digit BCD adder using two 1-digit BCD adders. Test the 2-digit BCD adder with the following test cases:

o        0 + 0

o        9 + 10

o        99 + 99

o        16 + 64

Save this project as 2digitBCD in the folder Lab4.

 What to turn in
  • Completed truth table in the Theory section.
  • All work related to the building of the Sum > 9? circuit. (Truth tables, K-maps, Boolean equations, etc., if any.)
  • 1digitBCD (.gdf, .scf)
  • 2digitBCD (.gdf, .scf)