COSC 6368 (Dr. Eick) in Fall 2016
Homework1 (Individual Homework)
Third Draft
Assigned: 10/1/2016
Last Updated: 10/6/2016
Due: 10/17/2016 at 11p
Problem 1: State-Space Search Representation
In the water-jug puzzle we are given a 3 liter jug, named Three, and a 4 liter jug,
named Four. Initially, Three and Four are empty. A jug can be filled from a tap T, and, we can
discard the water from either jug into a drain, D. Water may also be poured from one jug into another. There
are no other measuring devices. We want to find a set of operations that will leave precisely two liters
of water in Four.
(a) Formulate this problem as a state-space search problem
Give a precise definition of a state, the start state, the goal
state or goal condition, and the operators. Operators should be specified
as "schemas" that indicate for a given state, when the operator
is legal (i.e., a set of constraints on when the operator can be applied
to an arbitrary state) and the description of the successor
state after the operator is applied. In other
words, each operator should be specified in a way that it would easily implemented in a
program to solve this problem.
(b) Show the State Space
Draw the complete state-space graph that includes all nodes (and legal directed arcs
connecting these nodes) for this problem. Inside each node show the state description, and
label each arc with its associated operator. Highlight a path that gives a solution to the
problem.
Problem 2: Apply Various Search Techniques to the Same Search Problem
Assume that you have the following search graph, where S is the
start node and G1 and G2 are goal nodes. Arcs are labeled with
the cost of traversing them and the estimated cost to a goal
is reported inside nodes.
(i) For each of the search strategies listed below,
(a) indicate which goal state is
reached if any, (b) list, in order, the states expanded,
and (c) show the final contents of the OPEN and CLOSED lists. (Recall that a
state is expanded when it is removed from the OPEN list.)
When all else is equal, nodes should be expanded in alphabetical order.
- breadth-first
- depth-first
- best-first
(using f = h)
- A*
(using f = g + h)
- SMA* (using f=g+h and limiting the open-list to just 3 elements)
General Pseudocode for Searching
The following is the basic outline of the search strategy
used for breadth-first, depth-first, and best-first
search algorithms.
OPEN = { startNode } // Nodes under consideration.
CLOSED = { } // Nodes we're done with.
while OPEN is not empty
{
remove an item from OPEN based on search strategy used
- call it X
if goalState?(X) return the solution found
otherwise // Expand node X.
{
1) add X to CLOSED
2) generate the immediate neighbors (ie, children of X)
3) eliminate those children already in OPEN or CLOSED
4) add REMAINING children to OPEN
}
}
return FAILURE // Failed if OPEN exhausted without a goal being found.
The following is the basic outline of the search strategy
used for the A* and SMA*
search algorithms.
OPEN = { startNode } // Nodes under consideration.
CLOSED = { } // Nodes we're done with.
while OPEN is not empty
{
remove an item from OPEN based on search strategy used
- call it X
if goalState?(X) return the solution found
otherwise // Expand node X.
{
1) add X to CLOSED
2) generate the immediate neighbors (ie, children of X)
3) add all children to OPEN
}
}
return FAILURE // Failed if OPEN exhausted without a goal being found.
Problem 3: A* Termination
Algorithm A* does not terminate until a goal node is selected for expansion. However, a path to a goal node
might be reached long before that node is selected for expansion. Why not terminating as soon as the goal node is
found? Illustrate your answer with an example!
Problem 4: Comparision of Seach Algorithms
Compare Backtracking, Traditional Hill Climbing/Randomized Hill Climbing and Best-first Search!
What are the main differences between the three approaches?
Problem 5: Questions concerning Adversarial Search
(a) Assume alpha/beta search is applied to a game tree, such as the one in Fig. 5.2 of our
textbook using the following 2 versions v1 and v2:
(v1) enumerating leaf nodes from left to right
(v2) enumerating leaf nodes from right to left
Will versions v1 and v2 always select the same move, if there is a single
best move? Will version v1 and v2 always have the same runtime? Give reasons for your answers!
(b) Most game-playing programs do not save search results from one move to the next. Instead,
they usually start completely over whenever it is the machine's turn to move. Why?
(c) In real world games, such as checkers, it is usually not feasible to generate the entire search space. What approach is typically chosen by
game playing programs to cope with this problem?
(d) Why does search in game playing programs always proceed forward from the current position rather than backward from the goal?
Problem 6: Game Theory
(a) What is the Nash Equilibrium? After you found the Nash Equilibrium for a game what does it tell you about the game? If a game has no Nash
Equilibrium: what does it tell you about the game?
(b) Determine the Nash Equilibrium for the following 2-person game called Z:
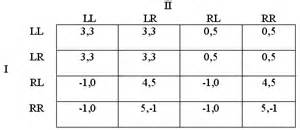
Problem 7: Planning
Assume the following state of the Boxworld is given:

Explain in detail (outlining all partial and complete plans generated and explaining why
they are generated and also giving the goal-subgoal tree(s) for the final plan) how a
STRIPS-like (or NOAH-like, if you prefer that) classical AI planning system
will come up with a plan that accomplishes the following goal, assuming that the depicted state is the initial
state:
on(B,D) and on(D,C)



