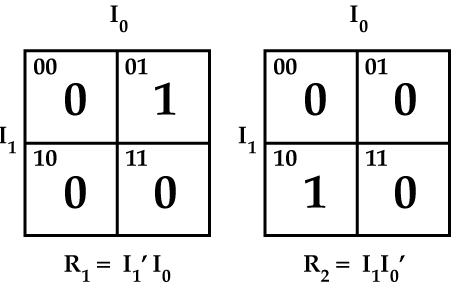Experiments

 

 

 

Experiment No. 5: Decoders and ALU

 

Objectives
  • In this lab, you will build a 2x4 Decoder and study its function.
  • You will then illustrate the usage of the decoder by designing and building a one-bit ALU that can perform any of the four operations: AND, OR, NOT, and ADD.
  • Finally, you will build larger ALUs by combining more than one smaller ALUs.

Discussion on Decoders

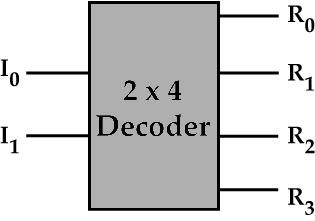
There are many instances where information is stored in a compact form and then expanded later to a more usable form. For example, information stored as a binary number is stored in its most compact form. When this information is expanded in a certain way, it can be used to activate a display that allows us to read the number in decimal. The process of expanding a compact form of information is called decoding. 

Another function of decoding is to use each unique binary number input to select a single unique output from among many choices. The block diagram and truth table for such a decoder are given below.


2x4 Decoder Block Diagram
 

Inputs

Outputs

I1 I0

R0

R1

R2

R3

0 0

1

0

0

0

0 1

0

1

0

0

1 0

0

0

1

0

1 1

0

0

0

1

2x4 Decoder Truth Table

In order to discover how to build this simple decoder, a sequence of Karnaugh Maps should be built. In fact, there should be one map for each of the four outputs of the decoder. However, we can immediately see that output R0 is a NOR function and output R3 is an AND function. Therefore, we will build maps for only output R1 and output R2.


Karnaugh Maps for Outputs R1 and R2


 

Discussion on ALU's

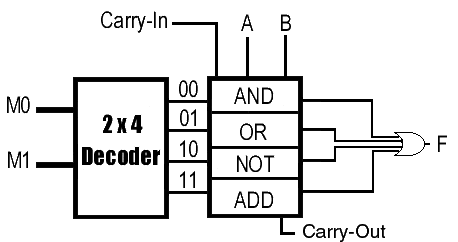
The Arithmetic and Logic Unit (ALU) is an important circuit in digital computers. It performs arithmetic and logic operations on its inputs. In this experiment you are supposed to design and implement a one-bit ALU that can perform any of the four operations: AND, OR, NOT, and ADD. Inputs to the ALU include Ai, Bi, Ci, M1, and M0, where Ai and Bi are the ith bits of operands A and B, Ci is the input carry when doing addition, and M1 and M0 are the control inputs which choose one out of the four operations to be performed on A and B. The mode selection is as follows:
 

AND if M1 M0 = 00. 

OR if M1 M0 = 01. 

NOT if M1 M0 = 10. 

ADD if M1 M0 = 11. 
 

Denote the outputs of the one-bit ALU by Fi and Ci+l, where Fi is the result of an operation and Ci+l is the carry out when the ADD operation is performed. The ALU can be decomposed into several functional blocks. A schematic block diagram of a one-bit ALU is shown below. Each functional block can be implemented separately. The ALU can then be built by properly combining all functional blocks together. 
 


ALU Block Diagram


 
 

 Prelab
  • Sketch the schematic diagram for the 2x4 decoder according to the block diagram above. Use only four 2-input AND gates and two NOT gates.


 

  • Sketch the schematic diagram for the 1-bit ALU according to the block diagram above. Remember, this 1-bit ALU represents the ith bit which means the carry-in does not have to be zero. As a result, the ADD function must be able to handle the carry-in. In other words, the half adder will not work here.


 

  • Sketch the block diagram for an n-bit ALU using the 1-bit ALU as building blocks.

 Procedure
  1. Using the schematic technique, build a circuit that implements the above 2x4 decoder (use kmaps). You can build it using only four 2-input AND gates and two NOT gates. Test your decoder by simulating the circuit and verifying its functionality. Save your 2x4 decoder as 2x4decoder in a folder (directory) called Lab5. Create a default symbol for your decoder for use in the next step.

 

  1. Using the 2x4 decoder you built in the previous step, design and implement a one-bit ALU according to the block diagram shown above. Save this as 1bitALU in a folder Lab5. Create a default symbol for your 1bitALU for use in the next step.


Note: The NOT function will apply to A only. The function for ADD will involve the bits Ai, Bi, Ci. The result will be stored in Fi and Ci+l. Ci+1 (carry-out) should produce a result only when the ADD function is selected; otherwise, it should be 0.

Test your one-bit ALU by simulating the circuit and verifying its functionality. To accomplish this, you must apply all eight possible input combinations to inputs Ai, Bi, Ci for each function (AND, OR, NOT, ADD) and verify Fi and Ci+l for each input combination.
 

  1. Computers usually have at least an 8-bit ALU which is constructed by combining more than one smaller capacity ALUs. This is done to simplify the design of the circuit and is known as bit-sliced designing. Combine two 1-bit ALUs properly to construct a 2-bit ALU. Check whether the functions work for two bits by simulating the circuit. Save this as 2bitALU in the folder Lab5.

 What to turn in
  • All truth tables and K-maps used to help build the circuits.
  • 2x4decoder, (.gdf, .scf)
  • 1bitALU, (.gdf, .scf)
  • 2bitALU, (.gdf, .scf)