Well-Connected Towns

Graph

Suppose we have an undirected graph G representing m roads (edges) connecting n towns (nodes), with edge weights describing the distances along the road in miles. Some of these towns have a bus station (call the number of towns with bus stations b). Each town with a bus station has buses that travel from that town along the roads, and have a one-way range of d miles: every town within d miles of road travel from this town through any number of other towns is reachable. A town is well-connected if it is reachable by bus from at least k towns (including itself, if it has a bus station) for some fixed number k. Given G, the list of b towns with bus stations, d, and k, determine the number of well-connected towns.

Expected runtime: O(b(n+m log m))

Hint: Consider the different variants of WhateverFirstSearch mentioned in the Graph Algorithms slides. Which one is most suitable?

Note on input:

All graphs will be given with nodes numbered from 0 to n-1, and edges will be provided in a list. For the above:

n - number of towns in the graph (integer)

m - number of roads in the graph (integer)

d - distance a bus can travel one-way (integer)

k - number of towns in order to consider well-connected (integer)

b - number of towns with bus stations (integer)

You may assume that all edge weights are greater than 0. The graph may not be connected.

n > b >= k

Format:

n

d

k

b

m

[ list of nodes with bus stations in a single line ]

[ list of edges, each line having the form SRC DST WEIGHT describing a single undirected edge between SRC and DST having weight WEIGHT ]

Output:

The number of towns which are well-connected

Example:

7
5
2
2
10
0 6
0 1 2
0 2 2
0 3 1
0 4 6
0 5 2
1 2 2
1 5 3
1 6 5
4 5 4
5 6 2

Output:
5

The graph is depicted in this image:

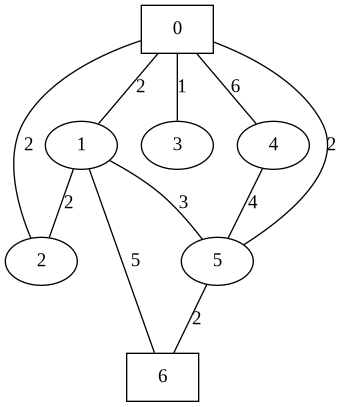
We can see that 0 can directly reach 1, 2, 3, and 5. It can reach 6 through 5. 4 is not reachable because the edge weight exceeds d = 5.