Reachable Islands

Graph

Suppose we have an archipelago of n islands which are connected in various ways by sandbars. The first island (n = 0) is home a species of elephants of varying sizes. The elephants want to roam the different islands, but each sandbar can only support up to a certain weight of elephant or they will sink. This can thus be represented as an undirected weighted graph, where the edges are sandbars and their weights are the maximum weight of elephant that can cross it.

Each elephant will visit every island they can reach given their own weight, crossing any number of sandbars that they are able to traverse.

For each island excluding the first island, determine the maximum weight of elephant that can reach that island.

Hint: It is possible to modify Dijkstra's algorithm to keep track of, instead of the shortest path distance, the highest minimum-sandbar weight path to that node from the start known at present. How would it be updated when you consider a new edge?

Note on input:

All graphs will be given with nodes numbered from 0 to n-1, and edges will be provided in a list. Edge weights depict the maximum weight elephant that can traverse that edge. You may assume that all edge weights are greater than 0 and less than 2^32

For the above:

n - number of islands (integer)
m - number of sandbars connecting islands (integer)




Format:

Input:
n
m
[ list of edges, each line having the form SRC DST WEIGHT describing a single undirected edge between SRC and DST having weight WEIGHT ]

Output:
For each of the n-1 islands excluding the first island, the maximum weight of elephant that can visit that island, in a single line, with spaces separating each number, and no trailing space after the last number


Example:
6
10
0 1 3
0 2 9
0 3 2
0 4 4
1 3 9
1 4 5
2 3 7
2 5 8
3 4 6
4 5 1

Output:
7 9 7 6 8

Explanation
The graph is depicted in this image:



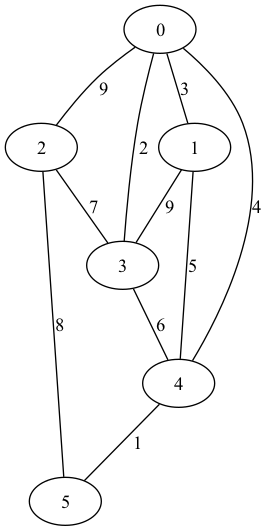
The optimal paths for supporting the heaviest possible elephants are given:
For island 1, the path from 0 to 2 to 3 to 1 will allow elephants up to weight 7 to cross.
For island 2, the direct link 0 to 2 will allow up to weight 9.
For island 3, 0 to 2 to 3 supports weight 7.
For island 4, 0 to 2 to 3 to 4 supports weight 6.
For island 5, 0 to 2 to 5 supports weight 8.