COSC 3340 – Introduction to Automata and Computing

Solution for Exercise Set 1

(Fall 2003)

Instructor: Dr. Rakesh Verma

TA: Razi A. Syed

Problem 1a

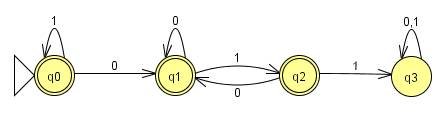
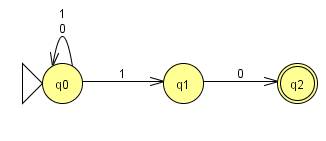
DFA for {w Є {0,1}* | w does not contain the sub string 011}

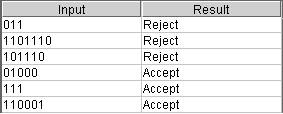
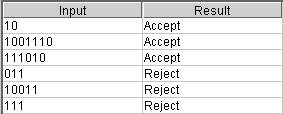
Test Results:

Problem 1b

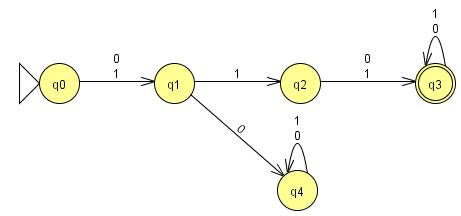
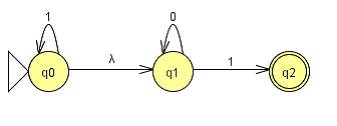
DFA for {w Є {0,1}* | w has length at least three and its second symbol is 1}

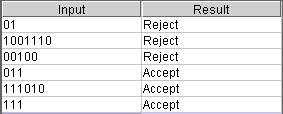
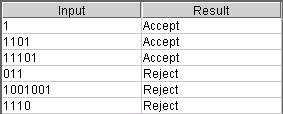
Test Results:

Problem 2

S = {a, b, c, d}

Binary Relation R = {(a, a), (a, d), (a, b), (b, a), (b, c)}

Reflexive Closure of R:

Before we can answer this question, we have to understand what Reflexive Relation means.

The formal definition of Reflexive Relation is:

A relation R on a set S such that xRx for every x in S.

The Reflexive Closure set will be all the elements in R, including the elements that are required for R to be closed under reflection. Therefore, the Reflexive Closure set is {(a, a), (b, b), (c, c), (d, d), (a, d),
(a, b), (b, a), (b, c)}

Symmetric Closure of R:

Again, we first need to understand Symmetric Relation.

The formal definition of Symmetric Relation is:

A relation R on a set S such that for every x and y in S, we have xRy iff yRx.

The Symmetric Closure Set of R is {(a, a), (a, d), (d, a), (a, b), (b, a), (b, c), (c, b)}, as this set is closed under R.

Transitive Closure of R:

The formal definition of Transitive Relation is:

A relation R in a set S such that when we have xRy and yRz, we also have xRz for all x, y and z in S.

For our problem, the Transitive Closure of R is {(a, a), (a, d), (a, b), (b, a), (b, c), (a, c), (b, d), (b, b)}

Problem 3

Given:

and

where

M₁ = (Q₁, Σ, δ₁, s₁, F₁) and

M₂ = (Q₂, Σ, δ₂, s₂, F₂)

M = (Q, Σ, δ, s, F)

Q = Q₁ x Q₂

s = (s₁ x s₂)

δ = ((q₁, q₂), s) = (δ₁ (q₁, s), δ₂ (q₂, s))

F = F₁ x F₂

We need to prove: L(M) = L(M₁) Ç L(M₂)

One way to prove the above is by Contradiction.

Let us assume that our premise that L(M) is the intersection of L(M₁) and L(M₂) is not true,

i.e.

Assume: L(M) ¹ L(M₁) Ç L(M₂)

Based on the above assumption, we can derive two implications:

One is that if w Î L(M₁) and w Î L(M₂), then it is implied that w Ï L(M).

Second is that if w Î L(M), then it is implied that w Ï L(M₁) and w Ï L(M₂).

We need to get contradictions for both the implications, hence our proof will have two steps.

Step 1: Show that if w Î L(M₁) and w Î L(M₂), then it is implied that w Î L(M)

Let us choose a word “w” such that w Î L(M₁) and w Î L(M₂). Since w is in both languages, and we are assuming that M does not accept such words, therefore based on our assumption, w Ï L(M).

But if w Î L(M₁), then that means that there is a set of transitions δ₁*Î δ₁ such that

δ₁* (s₁, w) = f_f Î F₁

(In other words, there are transitions in δ₁ that accepts “w”)

Similarly, we will have transitions in δ₂ that accepts “w”.

i.e.

δ₂* (s₂, w) = f₂ Î F₂

From the way we have defined F, it implies that if a word ends up in F₁ and F₂, it has to end up in F also, which means that the word will be accepted by M.

i.e.

δ* ((s₁, s₂), w) = f Î F

Therefore, we have shown that if w Î L(M₁) and w Î L(M₂), then it is implied that w Î L(M), and we have a contradiction to our assumption.

Step 2: Show that if w Î L(M), then it is implied that w Î L(M₁) and w Î L(M₂)

Let us choose a word “w” such that w Î L(M). Based on our assumption, since w is in L, it will be rejected by both L(M₁) and L(M₂), i.e. w Ï L(M₁) and w Ï L(M₂).

If w Î L(M), then that means that there is a set of transitions δ*Î δ such that w will be accepted, and will end in state that belongs to the set of final states (F) for Q.

i.e.

δ* ((s₁, s₂), w) = f Î F

Now F is defined as F₁ x F₂, which implies that if we have a final state in F, it must also belong to both F₁ and F₂.

i.e. f Î F => f Î F₁ and f Î F₂.

Now if f Î F₁, it follows that w Î L(M₁). Similarly, f Î F₂ implies that w Î L(M₂). Hence we have shown that if w Î L(M), then it is implied that w Î L(M₁) and w Î L(M₂), and we have a contradiction to our assumption.

We have shown that in both implications of our assumption, we get a contradiction, therefore due to contradiction, our assumption must also be false.

i.e.

which implies that

L(M) ¹ L(M₁) Ç L(M₂) is not true.

L(M) = L(M₁) Ç L(M₂)

Hence we have proved that M generates the language that is the intersection of language generated by M₁ and M_2.

Problem 4a

NFA for {w | w ends with 10} with 3 states

Test Results:

Problem 4b

NFA for the Language 1*0*1 with 3 states

Test Results:

Problem 4c

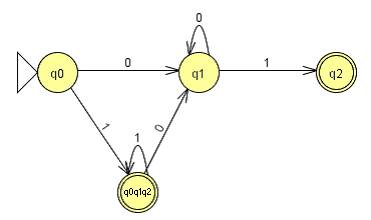
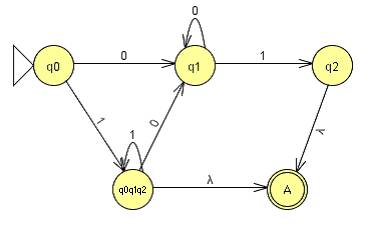
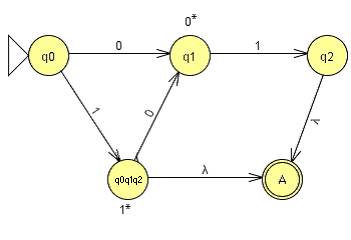
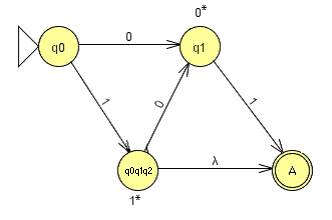
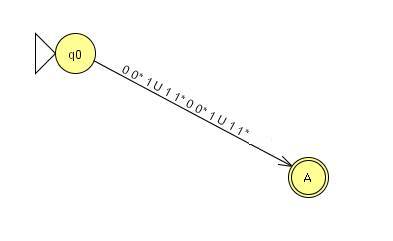
DFA by construction:

	0	1
q0 q2	q1	q0 q1 q2	0
q1	q1	q2	0
q0 q1 q2	q1	q0 q1 q2	1
q2	Æ	Æ	1
Æ	Æ	Æ	0

Regular Language by Construction:

Step 1: Draw out the Automata. Note that we can omit drawing the NULL state, as it will be eliminated eventually.

Step 2: Add a new and ONLY Final State “A” and make ε transitions from the final states in to this new final state.

Step 3: Change the loops to “*”.

Step 4: Start removing states one by one, by uniting and concatenating the string they would create.

After removing q2, we get:

After removing q0q1q2, we get:

Finally, after removing q1, we get:

The answer that we come up with is: (0 0* 1) U (1 1* 0 0* 1) U (1 1*), which looks a lot different from the original regular language given in 4b, but if we observe the language generated by this regular language, it is exactly the same.

Problem 5a

Given, L = {bⁿ a^m | m, n >= 0}, what is Suff(L)?

To solve this problem, first we have to understand what “Suffix” of a string is. Simply, suffix is the end characters of a string. There could be more than one suffix of a string.

For example, let us take a string, “texas”.

One suffix of this string could be “s”, or “as”, or “xas”.

The complete set of all suffixes for the string “texas” would be: {“s”, “as”, “xas”, “exas”, “texas”, ε}

Note that both the empty string, and the string itself are considered as suffix of the string.

Now let us observe the language L. It can generate any number of “b”s followed by any number of “a”s, and the empty string is included in the language. We are required to provide Suff(L), which will be a language that generates all the suffixes of each string by L.

By definition, we already know that Suff(L) will be at least be equal to, or a superset of L, as Suff(L) generates each word generated by L.

A few of the strings generated by L are ε, “a”, “ba”, “bba”, “bbba”, and so on.

If you notice, each string in the list is a suffix for the string ahead of it. There are many different possibilities of such lists, and L will accept each one of them. We can also take a few more examples, like “bbbbbaaaaa”, “aaaaa”, or “bbbbb”. L will accept all suffixes of each of these words.

If we notice carefully, we can conclude that the language L itself is capable of generating all the suffixes of any word it can generate. In fact, L can generate ANY sub string of any word it can generate. Therefore, one easy solution to our problem is: Suff(L) = L.

Problem 5b

Given that L is regular, prove or disprove that Suff(L) is regular.

One approach to solving this problem could be as follows:

Since we know that L is regular, we can design a DFA, M, which can accept all words in L. Now if we want our DFA, M, to accept any suffix of any string in L, only a small change to the DFA M will do that. What we need to do is introduce a new starting state, and make ε transitions from this starting state to each state already existing in the DFA M. After this change, the new NFA will accept all suffixes of the strings accepted by the language L.

Let us understand how this works with an example. Let us say that “texas” was accepted by L, and therefore we had transitions in the DFA, M, to accept “texas”. Now after introducing the new initial state with ε transitions to each state, lets say we wanted to accept “xas”. We can follow the ε transition to state where “x” initiated, and then follow the transitions to generate “a” and “s”, and accept the word.

After the change, we will have a new NFA M’, but the machine can still be converted to a DFA, and therefore the language it accepts is Regular. Since the language that M’ accepts is Suff(L), therefore Suff(L) is regular.

Formally,

Define DFA, M = (Q, Σ, δ, q₀, F) such that

L (M) = L

Define NFA, M’ = (Q’, Σ, δ’, q_s, F) as follows

and

Q’ = Q U { q_s } and

δ’ : δ U ({q_s} x {ε} x Q)

L(M’) = suff(L)