COSC 3340 – Introduction to Automata and Computing
Solution for Exercise Set 2
(Fall 2003)
Instructor: Dr. Rakesh Verma
TA: Razi A. Syed
|
Problem
1a |
||||
|
|
Regular Expression for {w
Є {0,1}* | the 0’s and 1’s alternate in w}. Solution: For this problem, there are two approaches. Either we can start by constructing the DFA or NFA, which will accept the language, and then do the construction, or we can simply try to write the Regular Expression directly. In this case, it is easier to actually write down the Regular Expression directly. We know that we want to have alternating 0’s and 1’s. This is basically (10)* or (01)*. The language also includes a single 0 or 1, and also the empty string. After carefully considering all possible cases, the regular expression for L is: ε U 0(10)* U 1(01)* U (10)* U (01)* |
|||
|
Problem
1b |
||||
|
|
Regular Expression for {w
Є {0,1,2}* | the 0’s and 1’s alternate in w}. Solution: Again we have the same two approaches. In this case, both approaches would work fine. In our required Language, it does not matter how 2’s occur in the middle, but 0’s and 1’s are always alternating. If we look at the solution in part 1a, all we need to do is to generate the 2’s appropriately. The required regular expression will be: 2* U 2*02*(12*0)*2* U 2*12*(02*1)*2* U
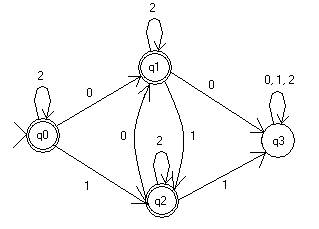
(2*12*02*)* U (2*02*12*)* We can also make the DFA, and do the construction.
The above DFA accepts the
required language. It does not matter how 2’s occur in the middle, but 0’s
and 1’s are always alternating. We need to convert the
above to GNFA, and then remove the states one by one. After the construction,
we end up with the following regular expression: 2* U 2*02* U 2*02*(12*0)*2* U 2*12* U
2*12*(02*1)*2* Note: There
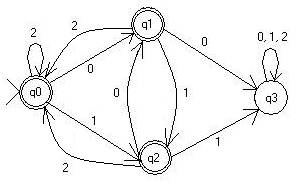
could also be a second interpretation of the given L. It could also mean that
if you see a 2, then the pattern is broken, and you will start over again
when you see a 1 or 0. An example would be 0102222010. From the first
interpretation, this word would be rejected. However, in the second one, it
will be accepted. The DFA in this case would be:
After the construction,
the Regular expression would be: 2* U (0(10)*2)* U (1(01)*2)* |
|||
|
Problem
2 |
||||
|
|
Prove in detail that the
language {w Є {0,1}* | w is of odd length and the middle symbol of w is
the same as the last symbol of w} is not regular. Solution:The language is of infinite length therefore the pumping lemma applies. Let us assume that the
language is regular. Since we are assuming that it is regular, it implies
that there must exist an Automaton with finite number of states that accepts
the language. Let us denote the number of states of that automaton by ‘p’. Now lets choose w = 10p10
p 1. Since w is of odd length, and the middle symbol 1, is the same as
the last symbol, we can say that w belongs to L. According to the
pumping lemma: |
|||
|
|
Here, |
W = 10p10
p 1 w = xyiz xy = 10p1 |
w Î L such that p ≥ |xy|
> 0 and i ³ 0 |
|
|
|
There are 3 possible
cases for xy. Case 1: y could contain only 1,
i.e. y = 1. In this case we need to find a value of i such that xyiz will not belong to L. If we
let i = 0, then w = xz = 0p10p1, which is not in L as
it is of even length. Therefore we have a contradiction. Case 2: y could contain 1 and some number of 0’s, i.e. y = 10m,
where p > m > 0. Again we need to find a value of i such that xyiz will not belong to L. If we
let i = 2, then w = xyyz = 10m10p10p1. Here,
the middle symbol of w is 0, which is not the same as the first symbol of w,
1.Therefore w is not in L and we have a contradiction. Case 3: y could contain only 0’s, i.e. y = 0m , where m
> 0. If we choose i = 2, then w = xyyz = 10p+m10p, which
is not in L as the middle symbol is 0, which is clearly not the same as the
beginning symbol 1. Hence we have a contradiction. Since we have shown contradiction in each case, therefore
it implies that our assumption was wrong. The only assumption made was that L
is regular, which was proven wrong. This proves that L is not regular. |
|||
|
Problem
3a |
||||
|
|
Give CFG for {w Є
{a,b}* | w is of odd length and the middle symbol of w is not the same as the
last symbol of w} Solution: We need to make sure of
two things: 1) w is of odd length and 2) middle symbol of w is the same as
the last symbol of w. We can have productions
of the form S->a X b, and X->a | b. This will ensure odd length, and we
also know the middle symbol. Obviously this example production does not take
care of all possible cases, but it does give us a basis to start with. Modifying
the above to ensure all possible ways of generating odd length strings, we
get the following productions: S-> a X b | b X a | a
X a | b X b | a | b The above CFG accepts all
odd length strings, and rejects everything else. The only thing left to do is
to make sure that the last symbol and the middle symbol is not the same. We
can do it by separating the productions at starting point as follows: |
|||
|
S -> S1 | S2
S1 -> a X a | b X a X -> a X b | b X a | a
X a | b X b | b S2 -> a Y b | b Y b Y-> a Y b | b Y a | a
Y a | b Y b | a |
(Last symbol is a) (Generate all odd, but
end only in b) (Last symbol is b) (Generate all odd, but
end only in a) |
|||
|
|
Note that the above
grammar does not generate the empty string, as it is not odd, and also does
not generate a or b by itself, as they are odd in length, but the middle and
last symbol would be the same. |
|||
|
Problem
3b |
||||
|
|
Give CFG for {w Є {a,b,c}*
| w has equal a’s and b’s} Solution: This CFG also needs to take care of all possible ways of combining a’s, b’s and c’s, making sure that for every a, we also generate b. One simple solution is: S -> a S b | b S a | SS
| S c | c S | ε |
|||