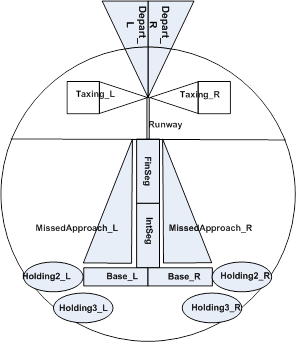
Logical Zones of RTL Model
SP:
(click to show/hide)
S_T1_ReqSeqNum(x)-T1_Approach_IAF2_L(x)<-6
E_T1_ReqSeqNum(x)-T1_Approach_IAF2_L(x)<-1
S_T1_ReqSeqNum(x)-S_T2_ReqSeqNum(x)<-1
S_T2_ReqSeqNum(x)-T2_Approach_IAF2_R(x)<-6
E_T2_ReqSeqNum(x)-T2_Approach_IAF2_R(x)<-1
E_T2_ReqSeqNum(x)-S_T3_ReqSeqNum(x)<-1
S_T3_ReqSeqNum(x)-T3_Approach_IAF3_L(x)<-6
E_T3_ReqSeqNum(x)-T3_Approach_IAF3_L(x)<-1
S_T3_ReqSeqNum(x)-S_T4_ReqSeqNum(x)<-1
S_T4_ReqSeqNum(x)-T4_Approach_IAF3_R(x)<-6
E_T4_ReqSeqNum(x)-T4_Approach_IAF3_R(x)<-1
T1_Approach_IAF2_L(x)-S_T1_Holding2_L(x)<-1
S_T1_Holding2_L(x)-E_T1_Holding2_L(x)<0
E_T1_Holding2_L(x)-S_T1_Base_L(x)<0
E_T1_Base_L(x)-S_T1_IntSeg(x)<0
E_T1_IntSeg(x)-S_T1_FinSeg(x)<0
S_T1_Base_L(x)-E_T1_Base_L(x)<-1
S_T1_IntSeg(x)-E_T1_IntSeg(x)<-1
S_T1_FinSeg(x)-E_T1_FinSeg(x)<-1
S_T1_Landing(x)-E_T1_Landing(x)<-1
S_T1_Taxing_L(x)-E_T1_Taxing_L(x)<-1
S_T1_MissedApproach_L(x)-E_T1_MissedApproach_L(x)<-1
E_T1_FinSeg(x)-S_T1_Landing(x)<0||E_T1_FinSeg(x)-S_T1_MissedApproach_L(x)<0
S_T1_Landing(x)-E_T1_FinSeg(x)<-1||E_T1_Landing(x)-S_T1_Taxing_L(x)<0
S_T1_Landing(x)-E_T1_FinSeg(x)<-1||E_T1_Taxing_L(x)-T1_Approach_IAF2_L(x)<20
S_T1_MissedApproach_L(x)-E_T1_FinSeg(x)<-1||E_T3_Holding3_L(x)-E_T1_MissedApproach_L(x)<-1
S_T1_MissedApproach_L(x)-E_T1_FinSeg(x)<-1||E_T3_Holding2_L(x)-E_T1_MissedApproach_L(x)<-1
T2_Approach_IAF2_R(x)-S_T2_Holding2_R(x)<-1
S_T2_Holding2_R(x)-E_T2_Holding2_R(x)<0
E_T2_Holding2_R(x)-S_T2_Base_R(x)<0
S_T1_IntSeg(x)-S_T2_Base_R(x)<0
E_T2_Base_R(x)-S_T2_IntSeg(x)<0
E_T2_IntSeg(x)-S_T2_FinSeg(x)<0
S_T2_Base_R(x)-E_T2_Base_R(x)<-1
S_T2_IntSeg(x)-E_T2_IntSeg(x)<-1
S_T2_FinSeg(x)-E_T2_FinSeg(x)<-1
S_T2_Landing(x)-E_T2_Landing(x)<-1
S_T2_Taxing_R(x)-E_T2_Taxing_R(x)<-1
S_T2_MissedApproach_R(x)-E_T2_MissedApproach_R(x)<-1
E_T2_FinSeg(x)-S_T2_Landing(x)<0||E_T2_FinSeg(x)-S_T2_MissedApproach_R(x)<0
S_T2_Landing(x)-E_T2_FinSeg(x)<-1||E_T2_Landing(x)-S_T2_Taxing_R(x)<0
S_T2_Landing(x)-E_T2_FinSeg(x)<-1||E_T2_Taxing_R(x)-T2_Approach_IAF2_R(x)<20
S_T2_MissedApproach_R(x)-E_T2_FinSeg(x)<-1||E_T4_Holding3_R(x)-E_T2_MissedApproach_R(x)<-1
S_T2_MissedApproach_R(x)-E_T2_FinSeg(x)<-1||E_T4_Holding2_R(x)-E_T2_MissedApproach_R(x)<-1
T3_Approach_IAF3_L(x)-S_T3_Holding3_L(x)<-1
S_T3_Holding3_L(x)-E_T3_Holding3_L(x)<0
E_T3_Holding3_L(x)-S_T3_Holding2_L(x)<-1
E_T3_Holding2_L(x)-S_T3_Base_L(x)<0
S_T2_IntSeg(x)-S_T3_Base_L(x)<0
E_T3_Base_L(x)-S_T3_IntSeg(x)<0
E_T3_IntSeg(x)-S_T3_FinSeg(x)<0
S_T3_Base_L(x)-E_T3_Base_L(x)<-1
S_T3_IntSeg(x)-E_T3_IntSeg(x)<-1
S_T3_FinSeg(x)-E_T3_FinSeg(x)<-1
S_T3_Landing(x)-E_T3_Landing(x)<-1
S_T3_Taxing_L(x)-E_T3_Taxing_L(x)<-1
S_T3_MissedApproach_L(x)-E_T3_MissedApproach_L(x)<-1
E_T3_FinSeg(x)-S_T3_Landing(x)<0||E_T3_FinSeg(x)-S_T3_MissedApproach_L(x)<0
S_T3_Landing(x)-E_T3_FinSeg(x)<-1||E_T3_Landing(x)-S_T3_Taxing_L(x)<0
S_T3_Landing(x)-E_T3_FinSeg(x)<-1||E_T3_Taxing_L(x)-T3_Approach_IAF3_L(x)<20
S_T3_MissedApproach_L(x)-E_T3_FinSeg(x)<-1||E_T1_Holding3_L(x)-E_T3_MissedApproach_L(x)<-1
S_T3_MissedApproach_L(x)-E_T3_FinSeg(x)<-1||E_T1_Holding2_L(x)-E_T3_MissedApproach_L(x)<-1
T4_Approach_IAF3_R(x)-S_T4_Holding3_R(x)<-1
S_T4_Holding3_R(x)-E_T4_Holding3_R(x)<0
E_T4_Holding3_R(x)-S_T4_Holding2_R(x)<-1
E_T4_Holding2_R(x)-S_T4_Base_R(x)<0
S_T3_IntSeg(x)-S_T4_Base_R(x)<0
E_T4_Base_R(x)-S_T4_IntSeg(x)<0
E_T4_IntSeg(x)-S_T4_FinSeg(x)<0
S_T4_Base_R(x)-E_T4_Base_R(x)<-1
S_T4_IntSeg(x)-E_T4_IntSeg(x)<-1
S_T4_FinSeg(x)-E_T4_FinSeg(x)<-1
S_T4_Landing(x)-E_T4_Landing(x)<-1
S_T4_Taxing_R(x)-E_T4_Taxing_R(x)<-1
S_T4_MissedApproach_R(x)-E_T4_MissedApproach_R(x)<-1
E_T4_FinSeg(x)-S_T4_Landing(x)<0||E_T4_FinSeg(x)–S_T4_MissedApproach_R(x)<0
S_T4_Landing(x)-E_T4_FinSeg(x)<-1||E_T4_Landing(x)-S_T4_Taxing_R(x)<0
S_T4_Landing(x)-E_T4_FinSeg(x)<-1||E_T4_Taxing_R(x)-T4_Approach_IAF3_R(x)<20
S_T4_MissedApproach_R(x)-E_T4_FinSeg(x)<-1||E_T2_Holding3_R(x)-E_T4_MissedApproach_R(x)<-1
S_T4_MissedApproach_R(x)-E_T4_FinSeg(x)<-1||E_T2_Holding2_R(x)-E_T4_MissedApproach_R(x)<-1
SA:
@(↑T
3Holding2_L,i)>@(↓T
1Holding2_L,i) ∧
@(↑T
1Holding3_L,i)>@(↓T
3Holding3_L,i) ∧
@(↑T
4Holding2_R,i)>@(↓T
2Holding2_R,i) ∧
@(↑T
2Holding3_R,i)>@(↓T
4Holding3_R,i) ∧
@(↑T
2Base_R,i)≥@(↑T
1IntSeg,i)∧
@(↑T
3Base_L,i)≥@(↑T
2IntSeg,i)+@(↑T
1IntSeg,i)∧
@(↑T
4Base_R,i)≥@(↑T
3IntSeg,i)+@(↑T
2IntSeg,i)+@(↑T
1IntSeg,i)
Results:
As explained in the LRTL algorithm, we prove the unsatifiability of the negation of (SP→SA) which is F=¬(¬SP→SA )=SP→¬SA. If F is unsatisfiable, then (SP→SA) is a theorem and the specifications of the system implies its safety assertions. Therefore, at this stage, we should negate the safety assertions. To do so, we convert the universal qualifier ? to the existential qualifier ? and negate the linear inequalities. Negation of a linear inequality can be obtained by converting the direction of the operands; for example, negation of the inequality -2f1+3f2-2f3 =0 is -2f1+3f2-2f3 <0 that can be transformed to 2f1-3f2+2f3≤1. As a result, negation of the safety assertions of the system is obtained as follows:
∃i@(↑T3Holding2_L,i)≤@(↓T1Holding2_L,i)∨
@(↑T1Holding3_L,i)≤@(↓T3Holding3_L,i)∨
@(↑T4Holding2_R,i)≤@(↓T2Holding2_R,i)∨
@(↑T2Holding3_R,i)≤@(↓T4Holding3_R,i)∨
@(↑T2Base_R,i)<@(↑T1IntSeg,i)∨
@(↑T3Base_L,i)<@(↑T2IntSeg,i)+@(↑T1IntSeg,i)∨
@(↑T4Base_R,i)<@(↑T3IntSeg,i)+@(↑T2IntSeg,i)+@(?T1IntSeg,i)
Now F=¬(SP→SA) is ready to be used as the input of Step 2 of the LRTL algorithm. As discussed, there are two rules in under LRTL method: all the equalities must be converted to inequalities; and inequalities must be in the normal form of a1.@(e1 ,i )±a2.@(e2 ,i )±…±an.@(en ,i )≤b . Therefore, conversion to the normal form is done before launching Step 3 of the algorithm. Step 3 indicates that the predicate logic must be transformed to the Presburger arithmetic formula to construct the FCNF .
After adding the timing properties obtained from debugging the specification of the system, a total of 76 propositional variables (events) and 108 positive propositional clauses are identified. The debugged system of linear inequalities AX =B has 131 rows and 76 columns. The debugged model has only one subsystem, which is the entire system of linear inequalities AX=B.
The generic solution [ a a ... a ] is obtained for row vector Λ1x131 =[ λ1 ... λ131 ] by solving Λ1x131A131x76=0. Positive row vectors Λ1x131=[ a a ... a] are identified such that a=1. Therefore, ΛB=-28a<0 can be held by replacing the variable a with any positive number. As the negative linear dependent of the system exists, the negative clause {¬A1,¬A2,...,¬A131} can be added to the set of negative clauses Fneg. Regarding the LRTL algorithm, the negative clause Fneg must be united with Fpos to build the propositional formula PF= Fpos∪Fneg. The unsatisfiability of the PF, which is the negation of SP→SA, requires that SP→SA is a theorem; the specification of the system implies its safety assertions.
Files:
The actual .txt file with the SP and negated SA used for this project is found
here.
A csv file containing the matrix generated by the LRTL verifications tool can be found
here.
An explanation of the tool we used and how it works is
here.
