Experiments

Experiment No. 7: Storage Elements

Objectives

• All the circuits that you have built up to this point have been combinational circuits. In combinational circuits the output depends only on the present value of the input. In this experiment, you will build circuits whose output depend on the present input and on the previous state of the circuit. These circuits are called sequential circuits. They are the building blocks of memory elements and state machines.

• In this experiment you will build flip-flops, and show how they can be used as memory elements or registers by simulating a series of arithmetic computations.

Discussion

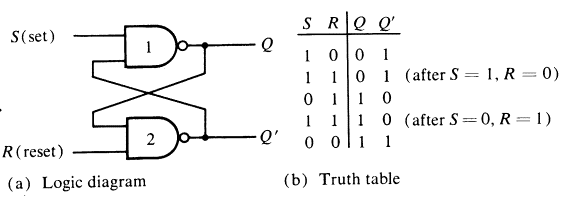
A latch is a combination of logic gates capable of storing one bit of information. It has a feedback loop which transfers the output information of the circuit back to its input. This loop causes the present latch state to depend on the previous latch state.

As a simple example, look at the RS latch below. The RS latch has only two inputs; the reset input (R) and the set input (S). We can build it by using two NAND gates as shown below.

Figure 7.1 RS Latch

Normally, both inputs are at 1 unless the value of Q is to be changed. An application of 0 to the set input causes output Q to go to 1 and Q’ to 0. After the set input returns to 1, an application of 0 to the reset input causes Q to become 0 and Q’ to 1.

The problem with the standard RS latch arises when both inputs are set to 0 at the same time. In that case both Q and Q’ go to 1. That is undesirable for two important reasons. First, we want the outputs Q and Q' to be always the complement of each other. Second, the latch will be in an unstable state: the value of Q becomes unpredictable when both inputs return to the normal value of 1.

There is a better way to represent a truth table for latches. The truth table below indicates a more natural notation:

S	R	Q(t+1)
0	0	Not Allowed
0	1	0
1	0	1
1	1	Q(t)

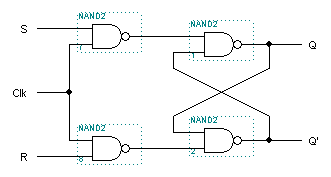
There is no need to list the value of Q’ because it is now truly the complement of Q. The notation Q(t) denotes the value of Q at time t, whatever that may be, at present. The notation Q(t+1) denotes the value of Q one unit of time later, that unit is defined by the clock period that drives the circuit. If the circuit is not controlled by a clock that unit can be thought of as the maximum amount of time the circuit takes to respond to the changes in inputs fully.

The next circuit diagram shows an RS latch with a clock input, Clk. When the clock input is a 0, the R and S inputs are converted into 1's before they reach the latch itself. From the previous truth table, you can see that this action prevents the latch from changing states because the "store" inputs are selected. When the clock pulse arrives as a 1 on the Clk input, it allows both R and S inputs to arrive at the inputs to the latch at the same time. Note that the NAND gates on the clock portion of the circuit invert the inputs. The circuit and truth table for this latch, called the Gated RS Latch, are as follows:

Clk	S	R	Q(t+1)
0	0	0	Q(t)
0	0	1	Q(t)
0	1	0	Q(t)
0	1	1	Q(t)
1	0	0	Q(t)
1	0	1	0
1	1	0	1
1	1	1	Not Allowed

(a) Circuit

(b) Truth Table

Figure 7.2 Gated RS Latch

The gated RS latch above is useful for many applications. However, you encounter a troublesome situation when S=R=1. To remedy this situation, we can build a gated D latch by combining the S and R inputs into just one data input called D according the the following:

Clk	D	Q(t+1)
0	0	Q(t)
0	1	Q(t)
1	0	0
1	1	1

(a) Circuit

(b) Truth Table

Figure 7.3 Gated D Latch

As you can see from the truth table of the gated D latch above, the output Q merely tracks the value of the data input D while Clk=1. We can therefore use the idea of the gated D latch to build storage elements called registers to store the result of some operation that we can use later.

Prelab

• Since a flip-flop depends not only on the present values of the inputs but also on the particular state that it is in, it is important to be able to set the initial state. On the gated D latch, setting Q=0 is called clear. Sketch out how you would modify the gated D latch above so that it can be cleared. Implement it in such a way that the gated D latch is cleared whenever clear=1.

• The gated D latch shown above is said to be level sensitive because while Clk=1, the output Q tracks the value of input D. However, it is also possible to design circuits that changes only at the point in time when the clock changes from one value to another. These type of circuits are called edge triggered. Using two gated D latches with clear, sketch out how you would connect the two in master-slave configuration to produce a positive-edge triggered D Flip-Flop.

• A register is merely a set of n flip-flops used to store n bits of information, where a common clock is used for each flip-flop. Sketch out how you can connect four positive-edge triggered D Flip-Flops to create a 4-bit register.

Procedure

1. Construct the gated D latch with clear capability and save it as d_latch in the directory Lab6. Compile and simulate the circuit to make sure it works according to the truth table in Figure 7.3(b). Also, make sure you simulate the clear functionality. As mentioned above, the gated D latch is level sensitive. Show how this is true by simulating what happens when the input D fluctuates several times while Clk=1. Click here to see a sample waveform of the gated D latch. Create a default symbol of the gated D latch for use in the next step.

2. Construct a positive-edge triggered D Flip-Flop by using two gated D latches and save it as d_edge_ff in the directory Lab6. Compile and simulate the circuit exactly as you have done with the gated D latch. Click here to see a sample waveform of the positive edge-triggered flip-flop. Note the difference between the edge-triggered D Flip-Flop and the gated D latch. Also note that the effect of the clear is not affected by the clock signal. This type of clear is called asynchronous clear. Create a default symbol of the positive-edge triggered D Flip-Flop for use in the next step.

3. Build a 4-bit register using four positive-edge triggered D Flip-Flops and save it as register in the directory Lab6. Compile the circuit and simulate the register to make sure it can indeed save some value. Click here to see a sample waveform of the 4-bit register.

4. Copy the 4-bit ripple-carry adder from Lab3 to the Lab6 folder. You will need to copy the following files:

• 4bitadder.gdf 
• fa.gdf 
• ha.gdf 

You can remove the c3 and c4 output tags from your 4-bit adder if you wish, however, you must set the carry-in or c0 to zero. You can easily do this by connecting a ground signal (symbol name gnd) to the c0 connector of your 4-bit adder. Recompile and create a default symbol for the 4-bit adder. 

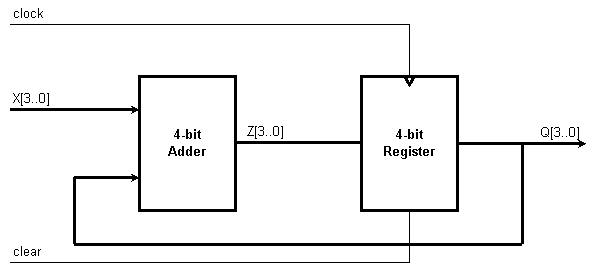
Create an adder with registered feedback by connecting the 4-bit adder to the 4-bit register according to the following block diagram and save it as feedback in the directory Lab7.

As you can see, this circuit basically adds some value X to whatever value Q is currently stored in the register. Simulate the following C program fragment using the adder with registered feedback:

x = 3;
x = x + 2;
x = x + 5;

Click here to see a sample waveform of the adder with registered feedback.

What to turn in

• d_latch, (.gdf, .scf)
• d_edge_ff, (.gdf, .scf)
• register, (.gdf, .scf)
• feedback, (.gdf, .scf)