( AB + A'B')( CD' + C'D )

(a)
F = wx' + y'z' + w'yz'
F'= (w' + x)(y + z)(w + y' + z)
(b)
F =(5,6,9,10) = w'xy'z + w'xyz' + wx'y'z + wx'yz'
F'= (w + x' + y + z')(w + x' + y' + z)(w' + x + y + z')(w' + x + y' + z)
(a)
F = AB' + ABD + ABD' + A'C'D' + A'BC'
F'= A'B'D + A'C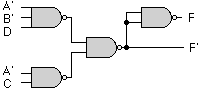
(b)
F =
(5,6,9,10) = w'xy'z + w'xyz' + wx'y'z + wx'yz'
F'= (w + x' + y + z')(w + x' + y' + z)(w' + x + y + z')(w' + x + y' + z)
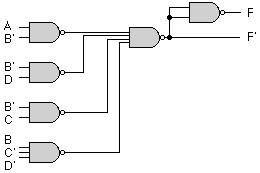
F = xy'z + x'yz +w
can be implemented by the following structure
![]()
For each of the three terms:
xy'z can be implemented by ![]() or
or ![]()
x'yz can be implemented by ![]() or
or ![]()
w can be implemented by ![]() or
or ![]()
By using different combinations of these, you will be able to implement the function with 2 X 2 X 2 = 8 different two-level gate circuits.
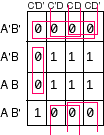
F(A,B,C,D) = ![]() (0,1,2,3,4,8,9,12)
(0,1,2,3,4,8,9,12)
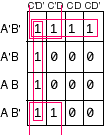
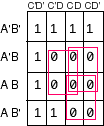
F = A'B' + C'D' + B'C'
F'= BD + BC + AC
NAND-AND
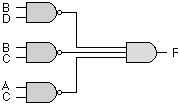
NOR-OR

F(A,B,C,D) = ![]() (0,1,2,9,11)
(0,1,2,9,11)
d(A,B,C,D) = ![]() (8,10,14,15)
(8,10,14,15)
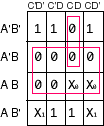
F'= B + A'CD
F = B'(A + C' + D')
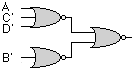
which can be simplified to
consisting of two NOR gates only
F(A,B,C,D) = ![]() (1,2,3,5,7,9,10,11,13,15)
(1,2,3,5,7,9,10,11,13,15)

F = D + B'C
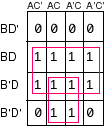
F = D + B'C