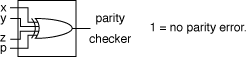|
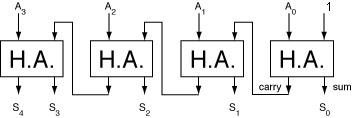
4-4 Design a combinational circuit that adds one to a 4-bit binary
number. For example, if the input of the circuit is 1101, the output is
1110. The circuit can be designed using four half-adders.
|
Let A3A2A1A0 + 1 = S4S3S2S1S0
|
|
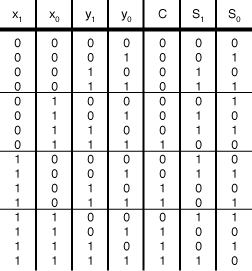
4-5 A combinational circuit produces the binary sum of two 2-bit
numbers, x1x0 and y1y0. The outputs are C, S1, and S0. Provide a truth
tableof the combinational circuit.
|

|
|
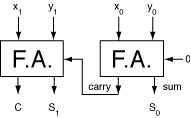
4-6 Design a circuit for the above problem using two
full-adders.
|
|
|
4-18 Derive the truth table of the circuit shown below.
|
F1 = A'B'C + A'BC' + AB'C' + ABC
F2 = AB + BC + AC
(Note: it is a full adder).
|
|
4-19 Draw the NAND logic diagram for each of the following
expressions using multiple-level NAND gate circuits:
|
(a)
(AB' + CD')E + BC(A + B)
= (AB' + CD')E + BC(A'B')'

(b)
w(x + y + z) + xyz
= w( x'y'z') + xyz

|
|
4-20 Convert the logic diagram of the code converter shown in Fig.
4-8 to a multiple-level NAND circuit.
|

|
|
4-22 Verify that the circuit shown below generates the exclusive-NOR
function.
|

|
|
4-24 Derive the truth table for the output of each NOR gate shown
below.
|
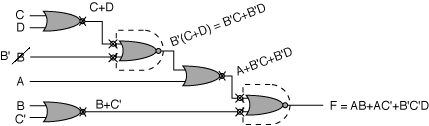
|
|
4-25 Prove the following equality.
|
x'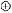 y = (x')'y + x'y' y = (x')'y + x'y'
= xy +x'y'
= (x'y + xy')'
= ( x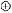 y ) y )
= x'y' + xy
= x'(y') + x(y')'
= x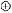 y' y'
|
|
4-26 Prove the following equality.
|
x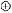 1 = x'•1 + x•1' = x'•1 + x•0= x'+ 0 = x' 1 = x'•1 + x•1' = x'•1 + x•0= x'+ 0 = x'
x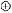 0 = x'•0 + x•0' = x'•0 + x•1= 0 + x = x 0 = x'•0 + x•0' = x'•0 + x•1= 0 + x = x
|
|
4-27 Show that if xy = 0 then x XOR y is equal to x+y.
|
If xy = 0 then
x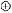 y = (x'y' + xy)' = (x'y' + 0)' = x + y y = (x'y' + xy)' = (x'y' + 0)' = x + y
|
|
4-29 Design the circuit of a 3-bit parity generator and the circuit
of a 4-bit parity generator using an odd parity bit.
|

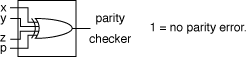
|






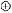 y = (x')'y + x'y'
y = (x')'y + x'y'y )
y'
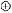 1 = x'•1 + x•1' = x'•1 + x•0= x'+ 0 = x'
1 = x'•1 + x•1' = x'•1 + x•0= x'+ 0 = x'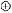 0 = x'•0 + x•0' = x'•0 + x•1= 0 + x = x
0 = x'•0 + x•0' = x'•0 + x•1= 0 + x = x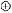 y = (x'y' + xy)' = (x'y' + 0)' = x + y
y = (x'y' + xy)' = (x'y' + 0)' = x + y