3-14 Draw a logic diagram using only two-input NAND gates to implement the following expression:	( AB + A'B')( CD' + C'D )
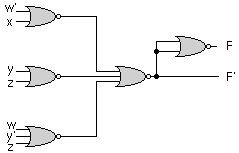
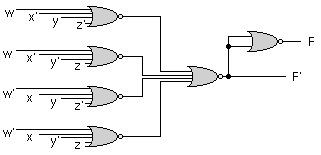
3-16 Implement the following functions with three-level NOR gate circuits.	(a) F = wx' + y'z' + w'yz' F'= (w' + x)(y + z)(w + y' + z)   (b) F = (5,6,9,10) = w'xy'z + w'xyz' + wx'y'z + wx'yz' F'= (w + x' + y + z')(w + x' + y' + z)(w' + x + y + z')(w' + x + y' + z)
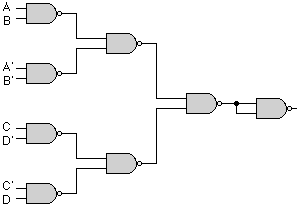
3-17 Implement the following expressions with three-level NAND circuits.	(a) F = AB' + ABD + ABD' + A'C'D' + A'BC' F'= A'B'D + A'C   (b) F = (5,6,9,10) = w'xy'z + w'xyz' + wx'y'z + wx'yz' F'= (w + x' + y + z')(w + x' + y' + z)(w' + x + y + z')(w' + x + y' + z)
3-19 Find eight different two-level gate circuits to implement F=xy'z+x'yz+w	F = xy'z + x'yz +w can be implemented by the following structure For each of the three terms: xy'z can be implemented by or   x'yz can be implemented by or   w can be implemented by or   By using different combinations of these, you will be able to implement the function with 2 X 2 X 2 = 8 different two-level gate circuits.
3-20 Implement the function F with the following two-level forms: NAND-AND, AND-NOR, OR-NAND, and NOR-OR.	F(A,B,C,D) = (0,1,2,3,4,8,9,12) F = A'B' + C'D' + B'C' F'= BD + BC + AC NAND-AND   NOR-OR
3-25 Implement the following Boolean function F together with the don't-care condition d using no more than two NOR gates. Assume that both the normal and complement inputs are available.	F(A,B,C,D) = (0,1,2,9,11) d(A,B,C,D) = (8,10,14,15) F'= B + A'CD F = B'(A + C' + D') which can be simplified to consisting of two NOR gates only
3-26 Simplify the following Boolean function using two differently constructed Karnaugh maps.	F(A,B,C,D) = (1,2,3,5,7,9,10,11,13,15) F = D + B'C F = D + B'C

COSC 3410 Answers to Selected Problems, Chapter | 1 | 2 | 3 | 4 | 5 | 6 | 7 |